Question

explain why you can take the compliment of the supplement of an angle, but you cannot take the supplement of its compliment

Answer 1

First, let's review the definition of complementary angles and supplementary angles.

Supplementary angles are two angles whose sum is 180 degrees while complementary angles are two angles whose sum is 90 degrees.

Let's say we have an angle theta, and this angle needs to be less than 90º, otherwise it wouldn't be possible to take its complement.

`\theta<90^(\circ)`

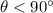
Now, let's take is complement and call it alpha. We know that

`\begin{gathered} \theta+\alpha=90^(\circ) \\ \Rightarrow\alpha<90^(\circ) \end{gathered}`

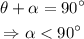
Now, let's take the supplement of alpha and call it Beta. We know that

`\alpha+\beta=180^(\circ)`

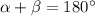
If we add theta to both sides of our equation, we have

`\begin{gathered} \alpha+\beta+\theta=180^(\circ)+\theta \\ (\alpha+\theta)+\beta=180^(\circ)+\theta \\ 90^o+\beta=180^(\circ)+\theta \\ \Rightarrow\beta=90^(\circ)+\theta \end{gathered}`

Since beta is the supplement of alpha, it must be less than 180º, and since we defined theta as an angle less than 90º, this constrain is fullfilled, and this means we can take the supplement of the compliment. Now, let's check the other way.

Let's define a new angle gamma. To take its supplement it just need to be lower than 180º.

`\gamma<180^(\circ)`

Let's take the supplement of gamma and call it mu.

We know that

`\begin{gathered} \gamma+\mu=180^(\circ) \\ \mu<180^(\circ) \end{gathered}`

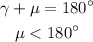
Now, let's take the complement of mu and call it sigma

We know that

`\begin{gathered} \mu+\sigma=90^o \\ \Rightarrow\sigma<90^(\circ) \\ and \\ \mu<90^(\circ) \end{gathered}`

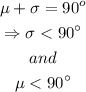
Since mu can be bigger than 90º, we cannot always take the complement of the supplement.