Question

Pls help I have a final in this number 5

Answer 1

To answer this question we will set and solve equations.

1) Notice that the angles that measure 2x+18 degrees and 3x-7 degrees are vertical angles. Since the lines with the marks are parallel, then:

`2x+18^(\circ)=3x-7^(\circ).`

Adding 7degrees-2x to the above result we get:

`\begin{gathered} 2x+18^(\circ)+7^(\circ)-2x=3x-7^(\circ)+7^(\circ)-2x, \\ 25^(\circ)=x. \end{gathered}`

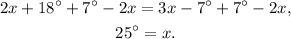
2) Notice that the angles that measure 78 degrees and y+10 degrees are corresponding angles. Since the lines with the marks are parallel, then:

`78^(\circ)=y+10^(\circ).`

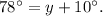
Subtracting 10 degrees from the above result we get:

`\begin{gathered} 78^(\circ)-10^(\circ)=y+10^(\circ)-10^(\circ), \\ 68^(\circ)=y. \end{gathered}`

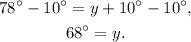
3) Recall that the interior angles of a triangle add up to 180 degrees, therefore:

`y+10^(\circ)+3x-7^(\circ)+d=180^(\circ).`

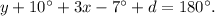
Substituting the above result we get:

`68^(\circ)+10^(\circ)+3(25^(\circ))-7^(\circ)+d=180^(\circ).`

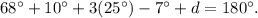
Simplifying the above result we get:

`146^(\circ)+d=180^(\circ).`

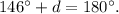
Therefore:

`d=34^(\circ).`

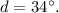
Answer:

`\begin{gathered} x=25^(\circ),\text{ vertical angles.} \\ y=68^(\circ),\text{ corresponding angles.} \\ d=34^(\circ),\text{ interior angles of a triangle add up to }180^(\circ). \end{gathered}`