Question

The muzzle velocity of bullets fired by German made military assault rifle G3 is 1790 mi/h. If the rifle is fired from a height of 5 ft parallel to the ground, determine the range of that bullet.

Answer 1

First of all, let us convert the given data into the standard units.

Velocity = 1790 mi/h

`\begin{gathered} v=1790*\frac{1\; km}{1.609\; \text{mile}}*(1000\; m)/(1\; km)*\frac{3600\; s}{1\; \text{hour}} \\ v=1790*(1000\cdot3600)/(1.609) \\ v=800\; (m)/(s) \end{gathered}`

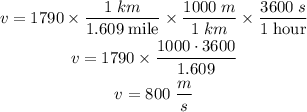
The bullet was fired from a height of 5 ft.

`\begin{gathered} s=5*(12\; in)/(1\; ft)*(2.54\; cm)/(1\; in)*(1\; m)/(100\; cm) \\ s=5*(12*2.54)/(100) \\ s=1.524\; m \end{gathered}`

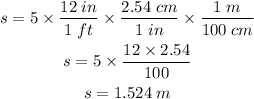
Now, we need to find out the time it takes for the bullet to reach the ground.

`s=u\cdot t+(1)/(2)gt^2`

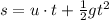
Where g is the acceleration due to gravity and u is the initial velocity of the bullet which must be zero since the bull was at rest initially.

`\begin{gathered} s=u\cdot t+(1)/(2)gt^2 \\ 1.524=0\cdot t+(1)/(2)\cdot9.81\cdot t^2 \\ 1.524=(1)/(2)\cdot9.81\cdot t^2 \\ t^2=(2\cdot1.524)/(9.81) \\ t^2=0.311 \\ t=\sqrt[]{0.311} \\ t=0.558\; s \end{gathered}`

The horizontal distance covered by the bullet is given by

`\begin{gathered} d=v\cdot t \\ d=800\cdot0.558 \\ d=446.4\; m \end{gathered}`

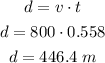
Therefore, the range of the bullet is 446.4 m

Or 1464.6 ft