Question

Stephen has graphed a circle centered at the origin and passing through the point (-30, -16). Because all circles are similar, he shrinks his circle so that the new circle's radius is half of the original size with the same center. What is the equation of the new circle?

Answer 1

Step 1: Write the formulae

`(x-a)^2+(y-b)^2=r^2`
`\begin{gathered} \text{where} \\ (a,b)\text{ is the center of the circle} \\ r=\text{ the radius of the circle} \end{gathered}`
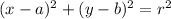
`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points on the Cartesian plane} \end{gathered}`

Step 2: Find the radius of the first circle

In this case,

`(a,b)=(0,0)`

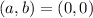
Since the circle passes through (-30,-16), then the distance between the center and (-30,-16) is the radius.

Let the radius be r. Then,

d=r, (x1,y1) = (0,0), and (x2,y2) = (-30,-16)

Therefore,

`r=\sqrt[]{(0-(-30))^2+(0-(-16))^2}=\sqrt[]{30^2+16^2}=\sqrt[]{900+256}=\sqrt[]{1156}`

Thus

`r=34`

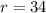
Therefore the radius of the new circle is 34 / 2 = 17

Step 3:

The new circle has radius 17 and center (0,0).

In this case,

r = 17

a = 0

b = 0

Therefore, the equation of the new circle is given by

`\begin{gathered} (x-0)^2+(y-0)^2=17^2 \\ x^2+y^2=289 \end{gathered}`