Question

Round the total of the areas under the standard normal curve to the left of Z

Answer 1

Explanation:

Step 1. We need to calculate the area under a normal curve given two z-values.

The first z-value is

`z_1=-1.61`

And the second z-value is:

`z_2=1.61`

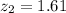
Note that these values are the same number but with different signs.

Step 2. In the following diagram we can see a representation of the two z-values shown in a normal curve:

Step 3. We need to find the area to the left of z1 and to the right of z2, these areas are shown in red:

Step 4. Using a z score table we can find the area to the left of a z-value, in this case, using a z score table we find that the area to the left of -1.61 is:

`P(z<-1.61)=0.0537`

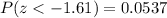
Step 5. In these cases when we have a symmetry of z-values (the same number with different signs) as in this case -1.61 and 1.61 the area to the right of 1.61 must be the same as the area to the left of -1.61. This is represented by:

`P(z>1.61)=0.0537`

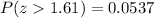
Step 6. We add the two areas to find the total red area under the curve:

`0.0537+0.0537=\boxed{0.1074}`

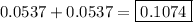
This result is already rounded to four decimal places.

Answer: 0.1074