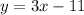Question

use the graph below write an equation of the line that passes through the given point and is parallel to the given line

Answer 1

Two lines are parallel if they have the same slope. Find the slope of the given line to write the equation of another line with the same slope. Then, use the fact that the point (3,-2) should belong to the line to find the equation of the line that we are looking for.

First, locate two points in the given line to calculate its slope. Notice that the points (1,-4) and (2,-1) belong to the line. Use the slope formula to find the slope of this line using the coordinates of these two points:

`\begin{gathered} m=(\Delta y)/(\Delta x) \\ =((-1)-(-4))/((2)-(1)) \\ =(-1+4)/(2-1) \\ =(3)/(1) \\ =3 \end{gathered}`

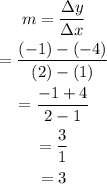
Then, the slope of this line is 3.

The equation of a line with slope m that passes through the point (x_0,y_0), in slope-point form, is:

`y=m(x-x_0)+y_0`

Substitute m=3 and (x_0,y_0)=(3,-2):

`\begin{gathered} y=3(x-(3))+(-2) \\ =3(x-3)-2 \end{gathered}`

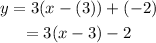
We can also write this equation in slope-intercept form by expanding the parenthesis and simplifying terms:

`\begin{gathered} y=3x-3(3)-2 \\ =3x-9-2 \\ =3x-11 \end{gathered}`

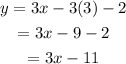
Therefore, the equation of the line that is parallel to the given line and passes through the point (3,-2) is:

`y=3x-11`