Question

Anderson uses the discriminant to correctly find the number of real solutions of the quadratic equation x2 + 4x + 8 = 0. Which explanation could Anderson provide?

The equation has no real number solutions because the discriminant is 0.

The equation has one real number solution because the discriminant is 0.

The equation has no real number solutions because the discriminant is less than 0.

The equation has two real number solutions because the discriminant is greater than 0.

Answer 1

B.) The equation has one real number solution because the discriminant is 0.

Explanation:

Answer 2

Option 3rd is correct

The equation has no real number solutions because the discriminant is less than 0

Explanation:

Discriminant(D)of a quadratic equation
`ax^2+bx+c = 0` is given by:

`D = b^2-4ac`

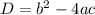
• If D = 0 , real zero of multiplicity 2.
• If D < 0, two zeros that are complex

• if D > 0, then two real zeros that are distinct.

As per the statement:

Anderson uses the discriminant to correctly find the number of real solutions of the quadratic equation:

`x^2+4x+8=0`

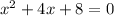
On comparing the given equation with
`ax^2+bx+c = 0` we have;

a = 1, b = 4 and c = 8

then;

`D = (4)^2-4(1)(8) = 16-32 = -16`

⇒
`D = -16 < 0`

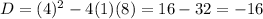
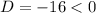
By definition;

Discriminant is less than 0

equation does not have real roots

Therefore, the equation has no real number solutions because the discriminant is less than 0