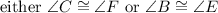We have two triangles ΔABC and ΔDEF. Since we don't have an image of the triangles we can make a diagram to represent them:
We are told by the problem that angle ∠D is approximately equal to angle ∠A. In the image, we represent in yellow these two equal angles:
It is also given by the problem that the segment AB is approximately equal to the line segment DE. These two equal sides are also represented in the image in color blue:
Also, segment BC is equal to the segment EF, shown in red in the following image:
Since we are asked for the triangles to be congruent using AAS (AAS is Angle Angle Side):
two angles and one side of each triangle have to be equal.
And so far, we have that one angle is equal and two sides are equal. So we just need that another of the angles of the triangles be equal, and we will meet the condition of two angles and one side (even if we have two equal sides, we need another angle to be equal to meet the AAS condition).
So we either can have ∠C equal to ∠F or
∠B equal to ∠E.
Either of those two options will give us the second equal angle that we need for the triangles to be congruent using AAS (angle angle side).
Thus, the answer is: