Question

Find the number of revolutions the tire makes during this motion, assuming no slipping

Answer 1

Given,

The initial velocity of the car, u=0 m/s

The final linear velocity of the car, v=28.7 m/s

The time duration, t=8.7 s

The diameter of the tires, d=50.1 cm=0.501 m

The radius of the tires is,

`\begin{gathered} r=(d)/(2) \\ =(0.501)/(2) \\ =0.25\text{ m} \end{gathered}`

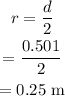
From the equation of motion,

`v=u+at`

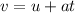
Where a is the acceleration of the car.

On substituting the known values,

`\begin{gathered} 28.7=0+a*8.7 \\ \Rightarrow a=(28.7)/(8.7) \\ a=3.3\text{ m/s}^2 \end{gathered}`

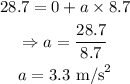
The angular acceleration of the tires is given by,

`\alpha=(a)/(r)`

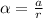
On substituting the known values,

`\begin{gathered} \alpha=(3.3)/(0.25) \\ =13.2\text{ rad/s}^2 \end{gathered}`

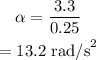
As the initial linear velocity of the car was zero, the initial angular velocity, ω₀ is also zero.

From the equation of motion,

`\theta=\omega_0t+(1)/(2)\alpha t^2`

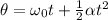
Where θ is the angular displacement of the tire.

On substituting the known values,

`\begin{gathered} \theta=0+(1)/(2)*13.2*8.7^2 \\ =499.55\text{ rad} \end{gathered}`

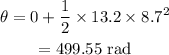
To complete one revolution, the tire has to rotate through 2π radians.

Thus the total number of revolutions made by the tires is,

`\begin{gathered} N=(\theta)/(2\pi) \\ =(499.55)/(2\pi) \\ =79.51\text{ } \end{gathered}`

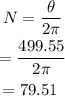
Therefore the total number of revolutions made by the tires is 79.51 which is approximately equal to 79.3202 in the option.