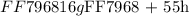Question

Rewrite in simplest terms: 4(-69 – 10h) + 3h = 4(-3h – 10g) Answer: Submit Answer

Answer 1

We are given a mathematical expression that needs to be simplified in the most meaningful form as follows:

`4\cdot(-6g\text{ - 10h ) + 3h -4}\cdot(-3h\text{ -10g )}`

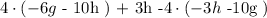
Whenever we are dealing with either an equation that needs to be solved or an expression that needs to be simplified we always refer to the rule of PEMDAS. The rule gives us the order in which mathematical operators are to be applied in decreasing order as follows:

`\begin{gathered} P\colon\text{ Parenthesis} \\ E\colon\text{exponents} \\ M\colon\text{ Multiplication} \\ D\colon\text{Division} \\ A-S\colon\text{Addition-Subtraction } \end{gathered}`

We will use the above rule and work through with the given expression for the process of simplification.

We will first solve the parenthesis for the entire expression as follows:

`4\cdot(-6g\text{ ) -4}\cdot(-10h\text{ ) + 3h -4}\cdot(-3h)\text{ -4}\cdot(-10g)`

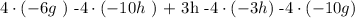
Then we apply the mathematical operation of M: Multiplication as follows:

`-24g\text{ + 40h + 3h + 12h + 40g}`

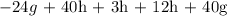
Now we will group the like terms i.e defined by a particular variable ( h or g ) and apply the A-S: Addition-Subtraction operator as follows:

`\begin{gathered} (40g-24g\text{ ) + ( 3h + 12h + 40h ) } \\ 16g\text{ + 55h} \end{gathered}`

The form expressed can not be further simplified as the variables ( h and g ) are expressed in the most simplified form i.e there is only one term for each variable. Hence, the algebraic expression is simplified to:

`\textcolor{#FF7968}{16g}\text{\textcolor{#FF7968}{ + 55h}}`