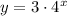Question

Find the exponential equation that goes to the points (2, 48) and (3, 192)

Answer 1

`y=3\cdot4^x`

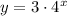
Explanation:

An exponential equation has the following form:

`y=a\cdot b^x`

We substitute each point to establish a system of equations:

`\begin{gathered} 48=a\cdot b^2\rightarrow a=(48)/(b^2) \\ 192=a\cdot b^3\rightarrow a=(192)/(b^3) \end{gathered}`

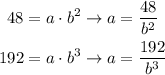
We can solve by equating both equations and solve for b:

`\begin{gathered} (48)/(b^2)=(192)/(b^3) \\ 48\cdot b^3=192\cdot b^2 \\ (b^3)/(b^2)=(192)/(48) \\ b=4 \end{gathered}`

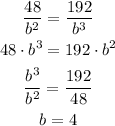
Now, we can calculate the value of a by substituting in the previous equations:

`\begin{gathered} a=(48)/(4^2)=(48)/(16) \\ a=3 \end{gathered}`

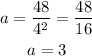
Therefore, the exponential equation of the points would be:

`y=3\cdot4^x`