Question

Is (x+5) a factor of f(x)=x^3 - 4x^2 + 3x + 7? Explain your reasoning

Answer 1

Step-by-step explanation:

Consider the following polynomial:

`f\mleft(x\mright)=x^3-4x^2+3x+7`

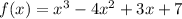
suppose by contradiction that (x+5) is a factor of the given polynomial f(x). This means that:

`f\mleft(x\mright)=x^3-4x^2+3x+7=(x+5)Q(x)`

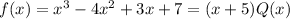
where Q(x) is another polynomial. Now, according to the above expression if we set f(x)=0, then we obtain:

`x^3-4x^2+3x+7=(x+5)Q(x)=0`

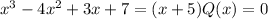
this is true when

`x+5=0`

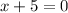
that is, when:

`x=\text{ -5}`

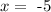
this means that x= -5 is a root of f(x). In other words, this is the same to say that

`f\mleft(\text{ -5}\mright)=0`

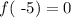
But this is a contradiction since:

`f\mleft(\text{ -5}\mright)=(\text{ -5})^3-4(\text{ -5})^2+3(\text{ -5})+7=\text{ -233}\\e0`

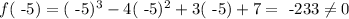
then, we can conclude that the expression (x+5) is not a factor of f(x).

Thus, the correct answer is:

Answer:

Since f( -5) is not equal to 0, we can conclude that (x+5) is not a factor of f(x).