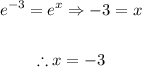Question

Convert the natural logs to exponential form, and solve. If 1n e^-3 = x then x = ?

Answer 1

The natural logarithm of a number is defined as follows:

`\ln A=x_{}`

means that when we elevate the Euler number e to x, the result is A:

`\ln A=x\Rightarrow A=e^x`

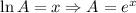
In this problem, we have

`A=e^(-3)`

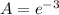
Thus

`\ln e^(-3)=x\Rightarrow e^(-3)=e^x`

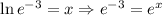
Then, since the bases are the same, for the equation to hold we need the exponents to be the same:

`\begin{gathered} e^(-3)=e^x\Rightarrow-3=x \\ \\ \therefore x=-3 \end{gathered}`