Question

Find the possible equations for the exponential function show (pic attached)

Answer 1

The Solution:

Given the graph below:

We are required to find the possible equation for the exponential function represented by the given graph.

The required exponential function can be obtained by the formula below:

`y=a(b)^x\ldots eqn(1)`

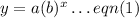
Apply the initial values indicated in the given graph.

That is, (0,60), this means when x = 0, y = 60

Substituting these values in the formula above, we get

`\begin{gathered} 60=a(b)^0 \\ 60=a\text{ ( since any number raised to the power of zero is equal to 1 )} \\ a=60 \end{gathered}`

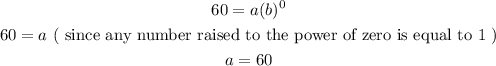
Similarly,

(2,15), this means when x = 2, y = 15

Substituting these values in the formula, we have

`\begin{gathered} 15=a(b)^2 \\ \text{ Recall:} \\ a=60 \\ \text{ Substituting 60 for a, we get} \\ 15=60b^2 \end{gathered}`

Dividing both sides by 60, we get

`\begin{gathered} (15)/(60)=(60b^2)/(60) \\ \\ (1)/(4)=b^2 \end{gathered}`

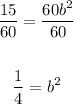
Taking the square root of both sides, we get

`\begin{gathered} \sqrt[]{b^2}=\sqrt[]{((1)/(4)}) \\ \\ b=\pm(1)/(2)=\pm0.5 \end{gathered}`

So, the exponential function is:

`y=60(\pm0.5)^x`

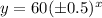
Therefore, the correct answer is [option 1]