Question

4.A mass-less rod is attached to a wall via a pivot point, asshown to the right. A rope, set an angle of 30 degrees tothe wall, holds up the rod. The rope is attached 3r from thewall. Meanwhile, there are two boxes, both 8 kgs,attached at r and 2r respectively.a.How much torque, in terms of r, do the two boxesgenerate together?30°ropewallrodr2r3r8 kg8 kgb. If the system is stable, then how much upwardstorque must the rope be generating, in terms of r?C.Calculate the tension in the rope, in terms of r.d. If the mass-less rod was swapped for a rod with mass, how would that affect the tension of therope, assuming the system stayed at rest? Briefly explain.

Answer 1

Given:

The angle made by the rope with the wall, θ=30°

The masses attached to the rod, m=8 kg

The distance between the pivot and the point where the rope is attached to the rod is 3r.

The masses are attached to the rod at r and 2r.

To find:

a. The total torque applied to the rod by the masses.

b. The torque that should be applied by the rope in order for the system to be stable.

c. The tension in the rope.

d. What happens if the massless rod is replaced with a rod having a mass.

Step-by-step explanation:

The torque is given by the product of the force applied and the distance between the point where force is applied and the pivot point.

The torque applied by the masses is given by,

`\begin{gathered} \tau_m=mg* r+mg*2r \\ =3mgr \end{gathered}`

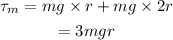
Where g is the acceleration due to gravity.

On substituting the known values in the above equation,

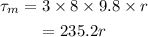
`\begin{gathered} \tau_m=3*8*9.8* r \\ =235.2r \end{gathered}`

b.

If the system is stable, then it is said to be in rotational equilibrium. Thus the net torque on the system is zero. Thus the rope needs to apply a torque equivalent to the torque applied by the masses but in the opposite direction.

Thus the upward torque applied by the rope is 235.2r.

c.

From the diagram, the torque is applied to the rod by the vertical component of the tension in the string.

Thus the torque applied by the rope is given by,

`\tau_m=T\cos\theta*3r`

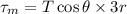
Where T is the tension in the string.

On substituting the known values,

`\begin{gathered} 235.2r=T*\cos30\degree*3r \\ \implies T=(235.2)/(3*\cos30\degree) \\ =90.5\text{ N} \end{gathered}`

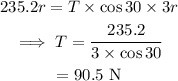
d.

If the massless rod is swapped for a rod with a mass, then the net downward torque on the rod will increase as the total downward force acting on the rod is increased.

Thus the rope will have to apply a greater upward torque than before. This implies that the tension in the string will also increase.

Final answer:

a. The torque applied by the masses is 235.2r

b. The upward torque that must be applied by the rope is235.2r

c. The tension in the rope is 90.5 N

d. If the massless rod is swapped for a rod with the mass, the tension in the rope will increase.