Question

How does e work? I’m not quite sure how to do it

Answer 1

`\begin{gathered} a)\mathbf{C(x)=5.50x+12}\text{ (}\forall x\in\lbrack0,30\rbrack) \\ b)(8,56), \\ c)(16,100) \\ d)0\leq x\leq30 \\ e)\mathbf{12\leq C(x)\leq177} \\ f)\: Check\: the\: graph\: below,\: please \end{gathered}`

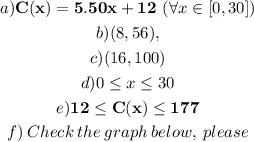
3)

a) Since the local towing company charges $5.50 per mile, and add to that a reservation fee of $12 for a maximum of 30 miles we can write out the following equation:

`\begin{gathered} \\ C(x)=5.50x+12,x\leq30 \end{gathered}`

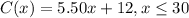
b) To determine C(8) is to evaluate the function

`\begin{gathered} C(8)=5.50(8)+12 \\ C(8)=56 \end{gathered}`

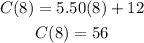
So for 8 miles, there's a cost of $56. We can write it out as (8,56)

c) Let's find out the number of miles that the company charges for $100:

`\begin{gathered} 100=5.50x+12 \\ 100-12=5.50x+12-12 \\ 88=5.50x \\ (88)/(5.50)=(5.50x)/(5.50) \\ x=16 \end{gathered}`

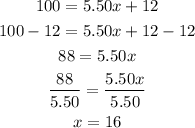
So $100 dollars is the price of towing a car for 16 miles. We have (16,100)

As the ordered pair.

d) The practical Domain, is the Domain of the function that in this case will only allow values for x in this interval: [0, 30] Because that towing company has restricted its mileage up to 30 miles:

`0\leq x\leq30`

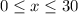
e) the range, will take into account the restriction of the Domain

`\begin{gathered} \mathbf{12\leq C(x)\leq177} \\ C(x)=5.50(0)+12=12 \\ C(x)=5.50(30)+12=177 \end{gathered}`

So if one person makes a reservation but in fact does not close the deal, at least the company makes $12. And, if a customer requests a 30 mile towing then the maximum profit will be $177

f) To construct a graph we need to write out a table for at least three values:

x | C(x) =5.5x +12

1 | 17.5

2 | 23

3 | 28.5

So the points we're going to locate are (1, 17.5), (2,23), and (3,28.5)

Since the slope is greater than 1, we can trace an increasing line passing through those points:

Note that in this graph there is not the practical Domain and Range, but rather the Domain and Range defined for the Real Set.

Hence, the answers are: