Step-by-step explanation:
We know that f(x) = - x² + x - 6
Then, we can find f(x + h) as follows:
f(x + h) = -(x + h)² + (x + h) - 6
f(x + h) = -(x² + 2xh + h²) + x + h - 6
f(x + h) = -x² - 2xh - h² + x + h - 6
Then, we can find the difference quotient as
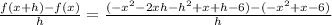
Simplifying, we get:
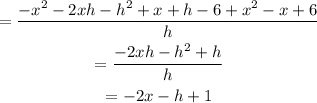
Therefore, the answer is
![undefined]()