1 Answer

Ben Von Handorf · Answer 1 · 2023-11-02T09:45:06+0000

Let

be the quadratic function that passes through the points (6,-3) and (3,0), then we get that:

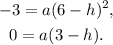
$\begin{gathered} -3=a(6-h)^2, \\ 0=a(3-h)\text{.} \end{gathered}$

Now, notice that a≠0 because y=a(x-h)² is a quadratic equation, therefore, from the last equation we get:

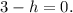
Adding h to the above equation we get:

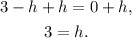
$\begin{gathered} 3-h+h=0+h, \\ 3=h\text{.} \end{gathered}$

Substituting h=3 in -3=a(6-h)² we get:

$-3=a(6-3)^2\text{.}$

Simplifying the above equation we get:

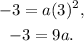
$\begin{gathered} -3=a(3)^2, \\ -3=9a\text{.} \end{gathered}$

Dividing the above equation by 9 we get:

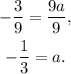
$\begin{gathered} -(3)/(9)=(9a)/(9), \\ -(1)/(3)=a\text{.} \end{gathered}$

Answer:

$y=-(1)/(3)(x-3)^2\text{.}$

Your comment on this question: