If x cameras are sold at price c each one, the total earning is $231, so we can write the following equation:
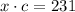
Then, if x+4 cameras are sold at price c-12 each one, the total earning is still $231, so we can write a second equation:
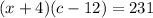
Let's equate the right sides of each equation, since they have the same value:
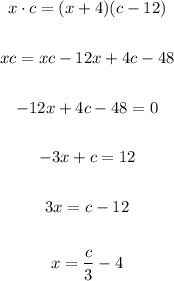
Now, let's use this value of x in the first equation and solve it for c:
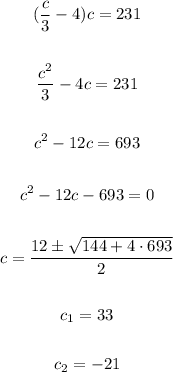
Since a negative cost is not valid, the answer is 33.