Question

60. take as much time as you need to solve a and b :)

Answer 1

Given:

The given function is y

`y=x^3-4x^2+2x-1`

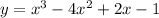
Find:

we have to find the equation of tangent line to the given curve at a = 2.

and then we have to draw the graph of the given curve and the tangent line.

Step-by-step explanation:

(a) we know the derivative of any curve represents the slope of the tangent line to the curve,

Therefore, firstly we will find the derivative

`\begin{gathered} y=x^3-4x^2+2x-1 \\ (dy)/(dx)=3x^2-8x+2 \\ at\text{ x =a= 2} \\ (dy)/(dx)=3(2)^2-8(2)+2=12-16+2=-2 \\ \end{gathered}`

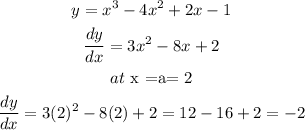
Therefore, slope of the tangent line is m = -2.

Now, the equation of the tangent line to the given curve is

`y=f^(\prime)(a)(x-a)+f(a)`

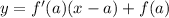
Now we have,

`\begin{gathered} f(a-2)=(2)^3-4(2)^2+2(2)-1=8-16+4-1=-5 \\ and\text{ f'\lparen a\rparen=-2} \end{gathered}`

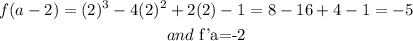
Therefore, the equation of tangent line is

y = -2(x-2) + (-5)

y = -2x+ 4 -5

y = -2x-1

(b) Now we will draw the graph of the given curve and tangent line to the given curve as follows

The graph of the curve is represented by blue colour and the graph of the tangent line is represented by green colour.