Question

Answer question number 20. The question is in the image.

Answer 1

• Amplitude: 0.5

,

• Period: 0.5

Explanation:

Given the function:

`g(x)=(1)/(2)\cos(4\pi x)`

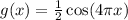
Amplitude

The amplitude of the general cosine function of the form y=Acos(Bx+C)+D is A.

Therefore, the amplitude of g(x) is 0.5.

Period

The period of the general cosine function of the form y=Acos(Bx+C)+D is determined using the formula:

`Period=(2\pi)/(|B|)`

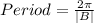
From g(x), the value of B = 4π, therefore:

`Period=(2\pi)/(|4\pi|)=(1)/(2)`

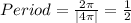
Graph

The graph of g(x) is given below:

Transformation

The parent function y=cos(x) has been vertically compressed by a factor of 1/2 and horizontally compressed by a factor of 4π.