Question

The equation (x – 5)²+(y - 1)² = p² represents circle A. The point (9,-2) lies on the circle. What is r, the length of the radius of circle A? 4√3 1√17 5

Answer 1

D. 5

Step-by-step explanation:

The equation of the circle is given as:

`\mleft(x-5\mright)^2+\mleft(y-1\mright)^2=p^2`

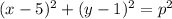
If the point (9,-2) lies on the circle, then:

`\begin{gathered} x=9 \\ y=-2 \end{gathered}`

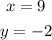
Substituting these into the equation above, we have:

`\begin{gathered} (x-5)^2+(y-1)^2=p^2 \\ (9-5)^2+(-2-1)^2=p^2 \\ (4)^2+(-3)^2=p^2 \\ 16+9=p^2 \\ p^2=25 \\ p^2=5^2 \\ p=5 \end{gathered}`

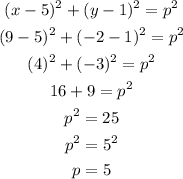
The general form of the equation of a circle is given as:

`\mleft(x-h\mright)^(2)+\mleft(y-k\mright)^(2)=r^(2)`

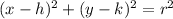
Comparing this with our given equation:

The radius of circle A, p =5.