Question

Verify the identity. Justify each step

Answer 1

Remember: We have to work from either the LHS or the RHS.
(Left hand side or the Right hand side)

You should already know this:

1.

`\boxed{\bf{\huge{tan \theta = (sin \theta)/(cos \theta)}}}<span>`

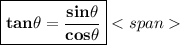
2.

`\boxed{\bf{\huge{cot\theta =(1)/(tan\theta)}}}`

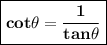
3.

`\boxed{\bf{\huge{sin^2\theta +cos^2 \theta = 1}}}}`

So, our question is:


`\sf{\huge{tan\theta + cot\theta=(1)/(sin\theta cos\theta)}}`

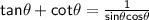
Plug in the first two identities I gave you.


`\sf{(sin\theta)/(cos\theta) +(1)/(tan\theta) =(1)/(sin\theta cos\theta)`

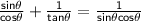
Apply the first identity I said you needed to know on 1/(tan θ). We should get:


`\sf{(sin\theta)/(cos\theta) +(1)/((sin\theta)/(cos\theta)) =(1)/(sin\theta cos\theta)}\\\\\\\sf{(sin\theta)/(cos\theta) +(cos\theta)/(sin\theta) =(1)/(sin\theta cos\theta)`

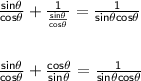
Multiply the first fraction by sinθ, on both the numerator and denominator.
Multiply the second fraction by cosθ, on both the numerator and denominator.


`\sf{(sin\theta * sin\theta)/(cos\theta * sin\theta) +(cos\theta * cos\theta)/(sin\theta * cos\theta) =(1)/(sin\theta cos\theta)}\\\\\\ \sf{(sin^2\theta)/(sin\theta cos\theta) + (cos^2 \theta)/(sin\theta cos\theta) = (1)/(sin\theta cos\theta)}\\\\\\\sf(sin^2\theta + cos^2\theta)/(sin\theta cos\theta) =(1)/(sin\theta cos\theta)}`
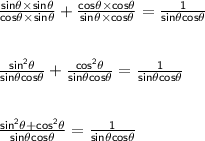
Now, use the third identity I said that you needed to know to simplify the numerator.


`\sf{(sin^2\theta +cos^2\theta)/(sin\theta cos\theta) =(1)/(sin\theta cos\theta)}\\\\\\\sf{(1)/(sin\theta cos\theta)=(1)/(sin\theta cos\theta)}`

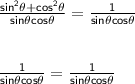
LHS = RHS

Therefore, identity is verified.