Question

What is the area of this figure?14 cm10 cm12 cm1cm3 cm1 cmOA. 46 sq cmOB. 44 sq cmOC. 62 sq cmOD 38 sq cm

Answer 1

We would like to know the area of this figure. WE first note that this figure is made of several figures, fortunately those figures are simple an we can calculate their areas with simple formulas.

First we note that the base of the figure is made of two triangles and one rectangle. We see that those triangles are the same and that their base is equal to 1 cm, whereas their height is 2 cm. Then the area of the base triangles is

`\begin{gathered} A=(bh)/(2) \\ =((1)(2))/(2) \\ =(2)/(2) \\ =1 \end{gathered}`

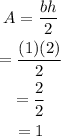
Then the area of the base triangles is 1 sq cm.

For the base rectable we note that its base is equal to 3 and its height is 2, then the area of the base rectangle is

`\begin{gathered} A=bh \\ =(3)(2) \\ =6 \end{gathered}`

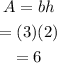
Therefore the area of the base rectangle is 6 sq cm.

Once we have the area of the parts of the base we add them to know the total area of the base. In our case we have 6+1+1 sq cm.

Therefore the area of the base of the figure is 8 sq cm.

We continue with our problem finding the area of the body of the figure, we see that it is a rectangle with base of 3 and height of 10. Then the area of the body is

`\begin{gathered} A=bh \\ =(3)(10) \\ =30 \end{gathered}`

Therefore the area of the body of the figure is 30 sq cm.

Finally, we have to calculate the area of the triangle in the upper part of the figure, we note that it has a base of 3 but we don't have the height yet. To find the height of this last triangle we see that from the base to its tip there is a distance of 14, we also note that the body rectangle has a height of 14. With this we conclude that the height of the upper triangle is 4. Then the area of the upper triangle is

`\begin{gathered} A=(bh)/(2) \\ =((4)(3))/(2) \\ =(12)/(2) \\ =6 \end{gathered}`

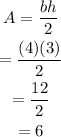
Therefore the area of the upper triangle is 6 sq cm.

To find the total area of the figure we just add the areas of the figures above. then

`A=8+30+6`

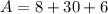
Then the area of the figure is 44 sq cm.