Given:
The function is

Required:
Find the x-intercepts and describe the end behavior of the graph of f(x).
Step-by-step explanation:
The given function is:
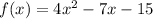
To find the x-intercepts put f(x)=0
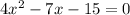
This is a quadratic equation solved by using the middle term splitting method.
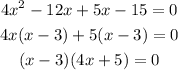
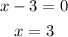
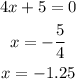
Thus the x-intercept are: -1.25 and 3.
Compare the given equation with the standard equation
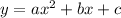

The vertex is (h,k).


Thus the vertex of the parabola is:
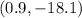
We will plot the points of the vertex and the x-intercepts and then draw the graph of the parabola as:
Here the leading coefficient a = 4>0
So the parabola opens upwards.
In the given function the degree is 2 which is even so as
![\begin{gathered} x\rightarrow\infty,\text{ f\lparen X\rparen}\rightarrow\infty \\ x\operatorname{\rightarrow}*-\infty,\text{f}\operatorname{\lparen}\text{X}\operatorname{\rparen}\operatorname{\rightarrow}\infty \end{gathered}]()
Final Answer:
As explained in the explanation part.