Question

In pic first balence and then solve question Part a.

Answer 1

Part 1. a.

42.1 g of silver chloride (AgCl).

Step-by-step explanation:

What is given?

Mass of silver nitrate (AgNO3) = 50.0 g.

Molar mass of silver nitrate (AgNO3) = 170 g/mol. (you can calculate this using the periodic table)

Molar mass of silver chloride (AgCl) = 143.4 g/mol.

Step-by-step solution:

First, let's balance the chemical equation by trial and error method:

`AgNO_3+BaCl_2\rightarrow AgCl+Ba(NO_3)_2.`

You can see that we have Cl and NO3 unbalanced, so if we put '2' moles beside AgCl, chlorine (Cl) will be balanced for both sides, but Ag would be unbalanced and NO3 too, so if we put '2' moles beside AgNO3, we will obtain the balanced equation:

Now, let's do the stoichiometry of part a.

Let's convert 50.0 g of AgNO3 to moles using its given molar mass:

`50.0\text{ g AgNO}_3\cdot\frac{1\text{ mol AgNO}_3}{170\text{ g AgNO}_3}=0.294\text{ moles AgNO}_3.`

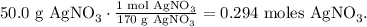
And now, let's see how many moles of AgCl are being produced by 0.294 moles of AgNO3. You can see in the chemical equation that 2 moles of AgNO3 reacted, produces 2 moles of AgCl, so the molar ratio is 2:2, more simply is 1:1. This means that if we're using 0.294 moles of AgNO3, we will obtain 0.294 moles of AgCl.

Based on this logic, the final step is to find the mass of AgCl in grams, using its molar mass, like this:

`0.294\text{ moles AgCl}\cdot\frac{143.4\text{ g AgCl}}{1\text{ mol AgCl}}=42.1\text{ g AgCl.}`

The answer is we will obtain 42.1 g of silver chloride (AgCl).