Question

We have the speed of the stones upon leaving the cannon, when both stones are in freefall with acceleration 10 m/s per second, regardless of mass. Thus the smaller stonegoes higher because it was launched with a greater initial speed.How much higher does it go? Using kinematics equations with zero final velocity,the height as a function of initial speed becomes x = v,?/2a. Since the initial speed issquared and in the numerator, doubling the speed increases the maximum height by afactor of 4. The small stone goes four times higher than the large stone

Answer 1

The speed of the smaller stone is given as two times the speed of the larger stone.

Let v be the initial velocity of the larger stone.

Then the initial velocity of the smaller stone is,

`v^(\prime)=2v`

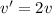
As the given kinematic equation is,

`x=(v^2)/(2g)`

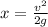
Where x is the distance travelled in the upward direction and g is the acceleration due to gravity.

For the smaller stone, the distance travelled is,

`\begin{gathered} x=(v^(\prime2))/(2g) \\ x=((2v)^2)/(2g) \\ x=4*(v^2)/(2g) \\ x=4*\text{distance travelled by the larger stone} \end{gathered}`

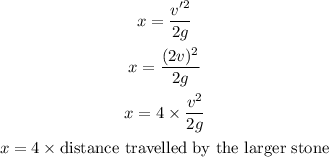
Thus, the distance travelled by the small stone in the upward direction is 4 times the distance travelled by the larger stone.