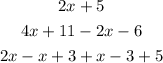The top alternatives have only two terms, one with x and one without it.
So, let's start by evaluating the whole expression until we get to two terms:
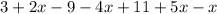
First, let's put like terms together.
The terms with x is one type of like terms and the terms withouth x is the other type. Mind the the front sign goes with the term:
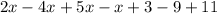
Now, we evaluate them:
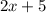
As we can see, we have got to the first alternative. Also, we have eliminated the second.
Now, let's reduce the other alternatives like this. If we got the same reduced form, it is equivalent.
Let's start by:
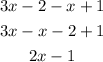
Doesn't match, so it is not equivalent.
The next:
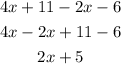
It matches, so it is equivalent.
Next:
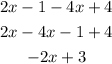
Doesn't match, so it is not equivalent.
Last one:
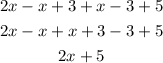
It matches, so it is equivalent.
Answer: The expressions that are equivalent are: