Question

Brooklyn has a goal to save $8,000 to buy a new entertainment system. In order to meet that goal, she deposited $4,132.79 into a savings account. If the account has an interest rate of 4.8% compounded quarterly, approximately when will Brooklyn be able to make the purchase?

Answer 1

Time=(log(8,000÷4,132.79)÷log(1+0.048÷4))÷4
Time=13.84 years rounded to 14 years

Answer 2

To see how much interest she'll get after a quarter:

$4132.79 + ($4132.79 × 0.048) = $4331.16

After two quarters:
$4331.16 + ($4331.16 × 0.048) = $4359.06

You can keep going until eventually reaching $8000 then see how many quarters has passed. That's a lot of calculator work!

There's another way that uses less calculation, but more algebra. I call it the exponential formula method! There's this general formula for stuff that increases exponentially, like virus, population, and MONEY:


`m= d {e}^(tc)`

M is money, d is deposit, t is time taken, and c is just some unknown constant related to the interest rate. There's also the natural logarithm form of this equation, which will come in handy later:


`ln( (m)/(d) ) = tc`

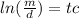
Alright first we gotta find that constant c for this equation to be useful! Let's plug in stuff we know.


`ln( (4331.16)/(4132.79) ) = (0.25)c`

We know how much she'll have after one quarter (0.25 years), and we know how much she deposited initially.

After pressing some buttons on the calculator we'll find that c = 0.1875.

Great! Now we can use that formula to find how many years (t) it'll take to reach M=$8000. To save time I'm going to use the natural log form:


`ln( (8000)/(4132.79) ) = t(0.1875)`

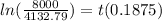
That will give us t = 3.522 which means it'll take approximately 3.5 years for her deposit to reach $8000!