To find the derivative of a composite function we use the chain rule
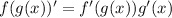
Then, we first find the derivatives of f and g. The function f is of the form
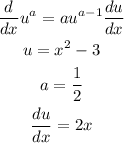
Then
![f^(\prime)(x)=(1)/(2)(x^2-3)^(-1/2)(2x)=\frac{x}{\sqrt[]{x^2-3}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/m6i3557hf6aspzhc54gx.png)
On the other hand, the derivative of g is very simple
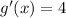
After doing this, we evaluate f' in g(x), and we have
![f^(\prime)(g(x))=\frac{4x-2}{\sqrt[]{(4x-2)^2-3}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ttdexn7tizzwsqky0qkx.png)
Replacing f'(g(x)) and g'(x) we obtain
![f(g(x))^(\prime)=f^(\prime)(g(x))g^(\prime)(x)\text{ = }\frac{4x-2}{\sqrt[]{(4x-2)^2-3}}\cdot4](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/1h1e86ts3vlawmqafqre.png)
Finally, we evaluate this expression in x=1
![(f\circ g)^(\prime)(1)=4\frac{4(1)-2}{\sqrt[]{(4(1)-2)^2-3}}=4\cdot\frac{2}{\sqrt[]{2^2-3}}=(8)/(1)=8](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/p0m7kg4ht6eqn60pyakm.png)
Then, the answer is 8