Question

Question 12. It is in the photo attached. It is related rates in calculus

Answer 1

We have to find the rate of the change of the water level at h = 6 m.

The exit rate is 5 ft³/min. This represents the (negative) change in volume of the cone.

If h is the water level, the rate of change of the water level will be its first derivative relative to time:dh/dt.

We also know that the cone will always have the same ratio between the radius of the base and the height. We will use itto recduce the number of variables in the equation.

Then, we can start by xpressing the volume for a certain value of h:

`\begin{gathered} V=(1)/(3)A_bh \\ V=(1)/(3)\pi r^2h \end{gathered}`

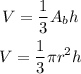
We have the volume in function of the height and the radius. As we know that radius and height will have a fixed proportion, we can use the initial values to find it: when the height is h = 10, the radius is 4, so we can write:

`\begin{gathered} (r)/(h)=(4)/(10)=(2)/(5) \\ r=(2)/(5)h \end{gathered}`

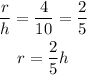
Replacing it in the volume formula, we get: