Question

Suppose a parabola has an axis of symmetry at x=-5, a maximum height of 9, and passes through the point (-7, 1) . Write the equation of the parabola in vertex form.

Please explain how it is solved. Thanks

Answer 1

The vertex-form of the equation of a parabola is
`y=a(x-h)^2+k`,
where (h, k) is the vertex point.

We are given that 9 is the maximum point, and that the axis of symmetry is the line x=-5.

The axis of symmetry passes through the vertex, so the x-coordinate of the vertex is -5. The maximum height is 9 means that the y-coordinate of the vertex is 9.

So: (h, k)=(-5, 9).


Substituting in the vertex-form, now we have:


`y=a(x+5)^2+9`.

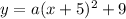
We also know that (-7, 1) is a point of the parabola, so this point is an (x, y) which satisfies the equation. That is:


`y=a(x+5)^2+9\\\\1=a(-7+5)^2+9\\\\a(-2)^2=-8\\\\4a=-8\\\\a=-2.`


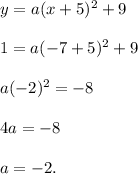
Now we have all the constants h, k and a, so we are able to write the equation:


`y=-2(x+5)^2+9`.


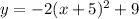
Answer:
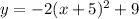
`y=-2(x+5)^2+9`.