Question

A container built for transatlantic shipping is constructed in the shape of a right rectangular prism. Its dimensions are 7 ft by 5 ft by 8.5 ft. The container is entirely full. If, on average, its contents weigh 0.21 pounds per cubic foot, and, on average, the contents are worth $8.80 per pound, find the value of the container’s contents. Round your answer to the nearest cent.

Answer 1

Given:

Dimensions are 7 ft by 5 ft by 8.5 ft

Contents weigh 0.21 pound

Contents worth $8.80 per pound

Find-: value of container contents.

Sol:

Volume is:

`\begin{gathered} Volume\text{ = }7*5*8.5 \\ \\ =297.5 \end{gathered}`

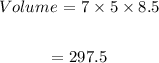
The formula of density is:

`\text{ Density =}\frac{\text{ Mass}}{\text{ Volume}}`

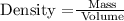
So,

`\begin{gathered} 0.21=\frac{\text{ Weight of contents in container}}{\text{ Volume of container}} \\ \\ 0.21=\frac{\text{ Weight}}{297.5} \\ \\ 0.21*297.5=\text{ Weight} \\ \\ \text{ Weight of contents in container = }62.475\text{ Pound} \end{gathered}`

Now $8.80 per pound

For 62.475 pounds the value is:

`\begin{gathered} =62.475*8.80 \\ \\ =549.78 \end{gathered}`

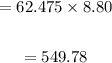
So the value of the container contents is 549.78