Question

Giving a test to a group of students, the grades and gender are summarized belowABCTotalMale481123Female62311Total10101434Give your answers as a fraction or decimal.If one student was chosen at random,(a) Find the probability that the student was male.(b) Find the probability that the student did NOT get an "B".(c) Find the probability that the student was male AND got a "C".(d) Find the probability that the student was male GIVEN they got a 'B'.(e) Find the probability that the student got a 'B' GIVEN they are male.

Answer 1

`\mathbf{a)(23)/(24)\: b)(12)/(17)\: c)(11)/(34)\: d)(4)/(5)\: e)(8)/(23)}`

a) For this question, Let's find the probability that a male student was randomly picked, note that there are 34 students, and the event male corresponds to 23 students

`P(\text{male)}=(23)/(34)`

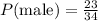
b) If the student did not get a B, we can include in this event all other grades so we can write using the complementary concept:

`P(\text{notB)}=1-(10)/(34)=(34)/(34)-(10)/(34)=(24)/(34)=(12)/(17)`

Note that subtracted the whole minus the ones who took B (10/34)

c) To find the male students that got C, we can write out:

`P(malegotC)=(11)/(34)`

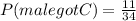
Note on the table the event male who got C: 11 students over the total number of students (34)

d) For this one there is a condition, male student given they got B we can write it this way:

`P=(8)/(10)=(4)/(5)`

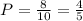
Note that for this case, conditional probability, we won't consider the total number of students, but the total number of students who got B and then find then on the numerator the event male.

e) Similarly, in this case, the subspace will be male students. So out of 23 we'll pick the ones who got B:

`P=(8)/(23)`

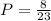
Then the answer is:

`\mathbf{a)(23)/(24)\: b)(12)/(17)\: c)(11)/(34)\: d)(4)/(5)\: e)(8)/(23)}`