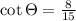Question

For the graph below what is the cos, tan, csc, sec, cot, sin.

Answer 1

Since the acute angle of the given angle lies in the 3rd quadrant then

sin, cos, sec, csc will give negative values and tan and cot will give positive values

Since we have the adjacent side = -8 and the hypotenuse = 17, then

We can find cos the angle first

`\cos \Theta=-(8)/(17)`

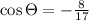
And sec is a reciprocal of cos (sec = 1/cos), then

`\sec \Theta=-(17)/(8)`

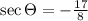
We will use the identity

`\sin ^2\Theta+\cos ^2\Theta=1`

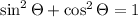
To find sin cita

`\begin{gathered} \sin ^2\Theta+(-(8)/(17))^2=1 \\ \sin ^2\Theta+(64)/(289)=1 \\ \sin ^2\Theta=1-(64)/(289) \\ \sin ^2\Theta=(225)/(289) \end{gathered}`

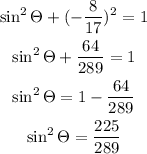
Take a square root of it to find sin and take the negative value

`\begin{gathered} \sqrt[]{\sin^2\Theta}=\pm\sqrt[]{(225)/(289)} \\ \sin \Theta=-(15)/(17) \end{gathered}`

As csc is the reciprocal of sin, then

`\csc \Theta=-(17)/(15)`

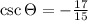
To find tan, we will use tan = sin/cos

`\begin{gathered} \tan \Theta=(\sin \Theta)/(\cos \Theta) \\ \tan \Theta=(-(15)/(17))/(-(8)/(17)) \\ \tan \Theta=(15)/(8) \end{gathered}`

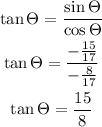
As cot is the reciprocal of tan, then

`\cot \Theta=(8)/(15)`