Question

Find the indefinite integral. (use c for the constant of integration.) sech8 x tanh x dx

Answer 1

`\displaystyle \int {sech^8(x)tanh(x)} \, dx = -(sech^8(x))/(8) + C`

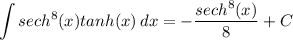
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Integration

• Integrals
• [Indefinite Integrals] Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

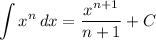
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

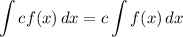
U-Substitution

Explanation:

Step 1: Define

Identify

`\displaystyle \int {sech^8(x)tanh(x)} \, dx`

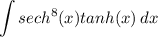
Step 2: Integrate Pt. 1

Identify variables for u-substitution.

1. Set u:
   `\displaystyle u = sech^8(x)`
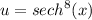
2. [u] Differentiate [Hyperbolic Differentiation, Chain Rule]:
   `\displaystyle du = -8sech^8(x)tanh(x) \ dx`

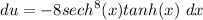
Step 3: integrate Pt. 2

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {sech^8(x)tanh(x)} \, dx = (-1)/(8)\int {-8sech^8(x)tanh(x)} \, dx`
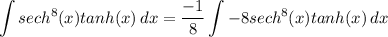
2. [Integral] U-Substitution:
   `\displaystyle \int {sech^8(x)tanh(x)} \, dx = (-1)/(8)\int {} \, du`
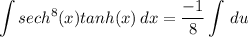
3. [Integral] Reverse Power Rule:
   `\displaystyle \int {sech^8(x)tanh(x)} \, dx = (-u)/(8) + C`
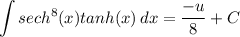
4. Back-Substitute:
   `\displaystyle \int {sech^8(x)tanh(x)} \, dx = -(sech^8(x))/(8) + C`

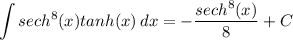
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration