Question

A population of bacteria is growing according to the equation p(t)=1000e^.04t. Estimate when the population will exceed 1455.

Answer 1

The given equation is:

`P(t)=1000e^(0.04t)`

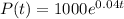
It is required to find when the population will exceed 1455.

To do this, substitute the given population and solve the resulting equation for t:

Substitute P(t)=1455 into the equation:

`1455=1000e^(0.04t)`

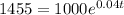
Solve the equation for t:

`\begin{gathered} \text{ Divide both sides by }1000: \\ (1455)/(1000)=(1000)/(1000)e^(0.04t) \\ \Rightarrow1.455=e^(0.04t) \\ \text{ Swap the sides of the equation:} \\ \Rightarrow e^(0.04t)=1.455 \end{gathered}`

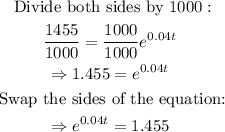
Take the natural logarithm of both sides:

`\begin{gathered} \Rightarrow0.04t=\ln1.455 \\ \Rightarrow t=(\ln1.455)/(0.04)\approx9.38 \end{gathered}`

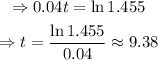
Hence, the population will exceed 1455 when t is about 9.38.

The population will exceed 1455 when t is about 9.38.