Answer:
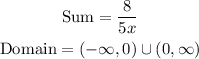
Step-by-step explanation
Given the sum of fraction;
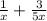
To get the domain of the function, we need to get all the input variable "x" for which the expression exists.
The function will exist when x ≠ 0 i.e. x < 0 and x > 0
The domain of the expression in interval notation is
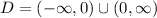
Solve the given expression
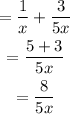
Hence the sum of the indicated operation is 8/5x