Solution
Step 1
Write out the equations representing each slide in the problem
Let the hat be = x
The golden rabbit = y
The briefcase = z
Hence
5x + y +3z = $237 .......................(1)
7x+7z= $371 ..................................(2)
8x + 3y + z = $320 .................(3)
Step 2
Solve the equations by substitution of the value of z from equation (2) into equation (1) and (3)
From (2)
7z = 371 -7x
z = (371-7x)/7
Substituting this value into equation (1) and (3) gives
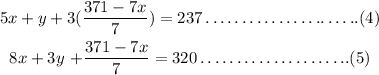
Step 4
Find the value of x and y by elimination method

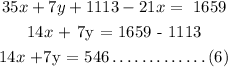
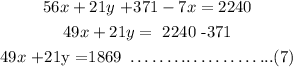
Subtracting equation 7 and 6 we have
3 x: 14x +7y = 546
1x : 49x +21y=1869
------------------------------
42x +21y =1638
49x +21y = 1869
----------------------------
-7x + 0 = -231
x = -231/-7 = $33= Price of one hat
Substituting this value of x into equation (7), we have
49(33) +21y = 1869
21y = 1869 -1617
21y = 252
y = $12= price of one gold rabbit
Step 5
Find the value of z using equation 1
From 1
5(33) + 12 + 3z = 237
177 +3z= 237
3z = 237 -177
3z= 60
z= 60/3
z= $20
Step 6
Find the value of
4x + 7y + 2z
4(33) + 7(12) +2(20) =132 +84 + 40 = $256