Question

Helpppp (answer is 38 i just need to show work)

Answer 1

`PQ=38`

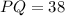
Step-by-step explanation

the perimeter of a triangle is the sum of the 3 lengths, so

`\text{Perimeter}=length_1+length_2+length_3`

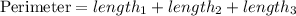
then,

Step 1

definde the perimeter of triangel SQT

`\begin{gathered} \text{Perimeter}=length_1+length_2+length_3 \\ Perimeter_(SQT)=SQ+QT+TS \\ \text{replace} \\ 135=(2x-4)+QT+TS\rightarrow equation(1) \\ \end{gathered}`

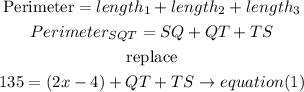
Step 2

definde the perimeter of triangle PQR

`\begin{gathered} \text{Perimeter}=length_1+length_2+length_3 \\ Perimeter_(PQR)=PQ+QR+RP \\ \text{replace} \\ 171=(x-9)+(2x-4)+QR+RP \\ 171=3x-13+QR+RP \\ 171+13=3x+QR+RP \\ 184=3x+QR+RP\rightarrow Equation\text{ (2)} \end{gathered}`

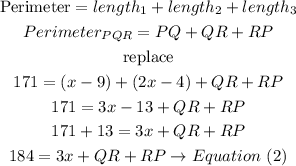
Step 3

as the triangles are congruent, the ratio of 2 perimeters must be the same, so

`\begin{gathered} (2x-4)/(2x-4+x-9)=(135)/(171) \\ 171(2x-4)=135(3x-13) \\ 342x-684=405x-1755 \\ 342x-405x=-1755+684 \\ -63x=-1071 \\ x=(-1071)/(-63) \\ x=17 \end{gathered}`

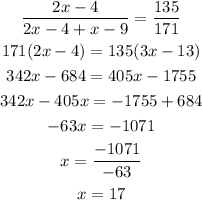
Step 4

finally, replace x in PQ to find the measure

`\begin{gathered} PQ=QS+SP \\ PQ=2x-4+x-9 \\ PQ=3x-13 \\ \text{replace} \\ PQ=3(17)-13 \\ PQ=38 \end{gathered}`

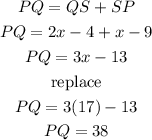
I hope this helps you