Question

Suppose f(x) is an exponential function that passes through the points

Answer 1

It is given that an exponential function passes through the points (-1,2/5) and (1,10).

It is required to find a formula for f(x).

Recall that an exponential function is a function given by an equation of the form:

`f(x)=a(b^x)`

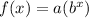
Where x is the exponent, a is a non-zero constant, the base b≠1 is a constant greater than zero.

The constants have to be calculated to find the formula for the exponential function.

To find the constants, substitute the given points into the equation of the function and solve the resulting system of equations:

Substitute (x,f(x))=(-1,2/5) into the equation of the function:

`(2)/(5)=a(b^(-1))`

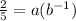
Substitute (x,f(x))=(1,10) into the equation of the function:

`10=a(b^1)`

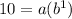
Make 'a' the subject of the first equation:

`\begin{gathered} (2)/(5)=a(b^(-1))\Rightarrow(2)/(5)=a((1)/(b)) \\ \Rightarrow(2)/(5)=(a)/(b) \\ \Rightarrow(2b)/(5)=a \end{gathered}`

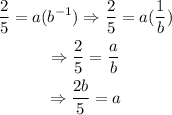
Substitute a=2b/5 into the second equation:

`\begin{gathered} 10=a(b^1);\quad a=(2b)/(5) \\ \Rightarrow10=(2b)/(5)(b^1)\Rightarrow10=(2b)/(5)(b)\Rightarrow10=(2b^2)/(5) \\ \Rightarrow2b^2=5*10\Rightarrow b^2=(5*10)/(2) \\ \Rightarrow b^2=25\Rightarrow b=\pm\sqrt[]{25}_{} \\ \Rightarrow b=\pm5 \end{gathered}`

Since as stated, the base, b must be greater than zero, it follows that b=5.

Substitute b=5 into the equation a=2b/5:

`\begin{gathered} a=(2b)/(5);\quad b=5 \\ a=(2\cdot5)/(5)=(10)/(5)=2 \end{gathered}`

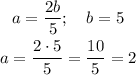
Substitute b=5 and a=2 into the original equation for an exponential function to get the required formula for f(x):

`f(x)=2(5^x)`

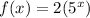
The required formula is f(x)=2(5ˣ).