Question

Reflect DEF across the y-axis. Then rotate D'E'F 90° counterclockwise around the origin. What are the coordinates of the vertices of D'E"F"? Show your work.

Answer 1

We will transform a generic point P=(x,y) and then apply both transformations to each of the points.

Reflection across the y-axis: the y coordinate stays the same, but the x-coordinate change its sign.

`(x,y)\longrightarrow(-x,y)`

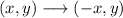
Rotation 90 degrees counterclockwise: Now we have the point after the first transformation (-x,y) and we have to rotate it 90 degrees counterclockwise. We can draw this as:

If A=(-x,y), the x-coordinate becomes the y-coordinate, and the y-coordinate becomes the x-coordinate, but of the opposite sign. Then, A'=(-y,-x).

Then, for each point (x,y) when both transformation applied we get:

`(x,y)\longrightarrow(-y,-x)`

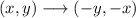
We have the points D, E and F: