ANSWER
B. 139.6 dB
C. 100 W/m²
Step-by-step explanation
B. From the first part, we have that the intensity of the Seattle roar was 45.7088 W/m². Now, the fans in Kansas City want to create a roar twice as intense,
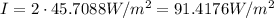
To find how many decibels this roar needs to be, we have to replace I with this value in the given equation,
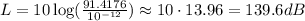
The fans in Kansas City have to roar at 139.6 dB.
C. Now, their roar was 140 dB and we have to find the intensity. In the given equation, replace L with 140,
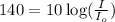
And solve for I. Divide both sides by 10,
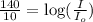
Rise 10 to the exponent of each side. By the rule of the exponent of the base of a logarithm, the result on the right side of the equation is what is in the parenthesis,
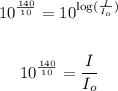
Finally, multiply both sides by I₀,
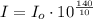
Replace the value of Io given and solve,
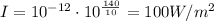
Hence, the intensity of the roar of the fans in Kansas City was 100 W/m².