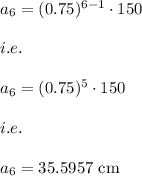Answer:
a)
The rule for the sequence is given by:
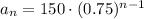
b)
The height of ball at the top of sixth path is:
35.5957 cm.
Explanation:
a)
Let the nth term of the sequence is represented by:
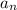
i.e. it represent the height of the ball in nth path.
It is given that:
You drop a ball from a height of 1.5 meters.
This means that the initial height of the ball is: 1.5 meters
We know that 1 meter= 100 centimeter(cm)
This means that:
1.5 meter= 150 cm.
Hence, we have:
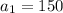
Also, Each curved path has 75% of the height of the previous path.
This means that:
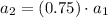

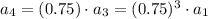
and so on.
Hence, we may write the nth term in general form by:
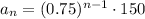
b)
The height of the ball at the top of sixth path.
i.e. the value of
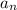 when n=6 is:
when n=6 is: