Question

Consider the quadratic function y=5(x-1)^2-4find the x intercepts

Answer 1

`\begin{gathered} x-\text{intercepts: } \\ x=\text{ 1+ }\frac{2}{\sqrt[]{5}}\text{ or x = 1- }\frac{2}{\sqrt[]{5}} \\ x\text{ = 1.894 or x = 0.106} \end{gathered}`Step-by-step explanation:

quadratic function: y = 5(x-1)² - 4

x intercept is gotten when y = 0

representing y with 0 in the quadratic function , we solve for x

0 = 5(x-1)² - 4

collect like terms by adding 4 to both sides:

0+ 4 = 5(x-1)² - 4 + 4

4 = 5(x-1)²

divide both sides by 5:

`(4)/(5)=(5\mleft(x-1\mright)^2)/(5)`

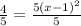
4/5 = (x-1)²

square root both sides:

`\begin{gathered} \sqrt[]{(4)/(5)}=\sqrt[]{(x-1)^2} \\ \pm\sqrt[]{(4)/(5)}=\text{ x-1} \end{gathered}`

simplify:

`\begin{gathered} x\text{ - 1 = }\pm\sqrt[]{(4)/(5)} \\ x\text{ =1}\pm\text{ }\sqrt[]{(4)/(5)}\text{ = 1}\pm\text{ }\frac{\sqrt[]{4}}{\sqrt[]{5}} \\ x\text{ = 1}\pm\text{ }\frac{2}{\sqrt[]{5}} \\ x\text{ = 1+ }\frac{2}{\sqrt[]{5}}\text{ or x = 1- }\frac{2}{\sqrt[]{5}} \\ x\text{ = 1+ 0}.894\text{ or x = 1-0.894} \\ x\text{in tercept: } \\ x\text{ = 1.894 or x = 0.106} \end{gathered}`