Question

Determine if the lines through each pair of points are parallel, perpendicular, or neither.(5, 10) and (1, 6), (2,-6) and (-1, -3)-parallel-perpendicular -neither

Answer 1

Answer:

Perpendicular

Step-by-step explanation:

Find the slope for the points (5, 10) and (1, 6)

`x_1=5,\text{ y}_1=10,\text{ x}_2=1,\text{ y}_2=6`

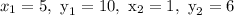
The slope is calculated below

`\begin{gathered} m_1=(y_2-y_1)/(x_2-x_1) \\ \\ m_1=(6-10)/(1-5) \\ \\ m_1=(-4)/(-4) \\ \\ m_1=1 \end{gathered}`

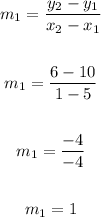
For the points (2,-6) and (-1, -3)

`\begin{gathered} m_2=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \\ m_2=(-3-(-6))/(-1-2) \\ \\ m_2=(-3+6)/(-3) \\ \\ m_2=(3)/(-3) \\ \\ m_2=-1 \end{gathered}`

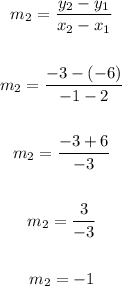
Note that:

`\begin{gathered} m_1m_2=1(-1) \\ \\ m_1m_2=-1 \end{gathered}`

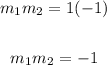
Since the product of the two slopes is -1, the lines through the pairs of points are perpendicular