Answer:
The 3rd graph represents the dilated image of the rectangle.
Explanation:
We are given the rectangle having vertices,
(1,-2), (1,2), (-1,2) and (-1,-2).
Now, this rectangle is dilated about the origin by the scale factor of
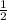
That is, the size of the rectangle is reduced by the factor
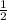 .
.
Then, the vertices of the new rectangle will be,
(1,-2) changes to
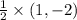 =
=
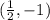
(1,2) changes to
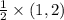 =
=
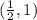
(-1,2) changes to
 =
=
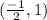
(-1,-2) changes to
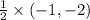 =
=
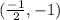
So, the vertices of the dilated rectangle are
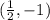 ,
,
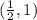 ,
,
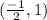 and
and
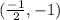 .
.
Thus, the 3rd graph shown below represents the dilated image of the rectangle.