Question

Solve each system of linear equation by adding or subtracting

Answer 1

We solve as follows:

2x - 4y = -10

3x + 4y = 5

------------------

5x = -5 => x = -1

Now, we replace the x in one of the initial equations:

3(-1) + 4y = 5 => -3 + 4y = 5 => 4y = 8 => y = 2

So, the solution for the system is the point (-1, 2), it can be seen in the following:

***

To be able and solve a system of equations there are multiple approaches, in this case, we will eliminate one of the variables in order to solve for the other and then find the missing one.

We can see that if we add both equations the y variable can be eliminated right away and we will be able to solve for x, that is:

`(2x-4y)+(3x+4y)=(-10)+(5)\Rightarrow5x=-5`
`\Rightarrow x=-1`

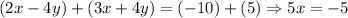
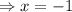
Now, we can use this value (Which is half the solution for the current problem) to find the value for y, that is:

`3(-1)+4y=5\Rightarrow-3+4y=5\Rightarrow4y=8`
`\Rightarrow y=2`

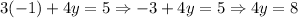
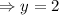
So, the solution is the point constructed from the x & y values found, that is that the solution is the point (-1, 2).

In the graph, we plot the functions and the only point in which they intersect is the solution:

Remember that some functions can have multiple intersection points (multiple solutions, or even infinite solutions) and also none at all.