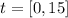Given the function;
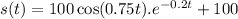
Part A:
We can find the change in the vertical position of the bungee jumper between t=0 and t=15 by subtracting the values derived after substituting the time values into the function.
When t=0
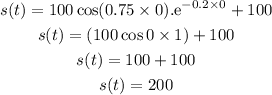
When t =15
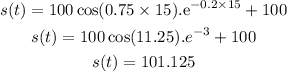
Therefore, the change in vertical position is
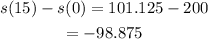
Answer:
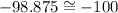
If we read the value of the graph, the answer also corresponds to -100.
Part B
The Jumper's average velocity would be given by
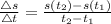
We would read off the graph by tracing the "t" values to their corresponding "s" values
For [0,15]
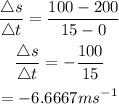
Answer:
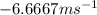
For [0,2]
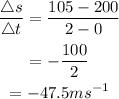
Answer:
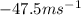
For [1,6]
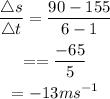
Answer:
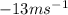
For [8,10]
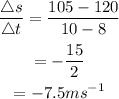
Answer:
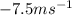
Part C
The bungee jumper achieves the highest average velocity at -6.6667m/s. Therefore the time interval would be;
Answer: