Question

Need help answering this question!!!The graph provided is the graph for f(x).

Answer 1

Given the function g(x):

`g(x)=-\sqrt[]{x+3}+2`

We see that the domain of g(x) is [-3, ∞), so it is not defined for values "behind" -3. For f(x), one part of the graph is a line joining the points (-5, 5) and (-1, -2). Then, we can calculate the slope of the line:

`m=(-2-5)/(-1+5)=-(7)/(4)`

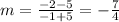
Then, for the general equation of the line (in slope-point form):

`f(x)=-(7)/(4)x+b`

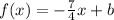
We use the point (-5, 5) to find the value of b:

`\begin{gathered} 5=(7)/(4)\cdot5+b \\ b=-(15)/(4) \end{gathered}`

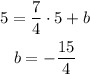
Now:

`f(x)=-(7x)/(4)-(15)/(4)`

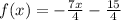
For -5 < x ≤ -1

Now, we solve the equation f(x) = g(x) for the linear part:

`\begin{gathered} -(7x)/(4)-(15)/(4)=-\sqrt[]{x+3}+2 \\ \sqrt[]{x+3}=(7x)/(4)+(23)/(4) \end{gathered}`

We take the square on both sides and solve the equation for x:

`\begin{gathered} 16x+48=49x^2+161x+529 \\ 49x^2+145x+481=0 \end{gathered}`

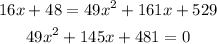
There are no real solutions for this quadratic equation, so the functions f(x) and g(x) do not "touch" each other on the linear part of f(x). Now, we analyze the parabolic part of f(x). We analyze the endpoints x = -1 and x = 6:

`\begin{gathered} f(-1)=-2 \\ f(6)=-5 \\ g(-1)=-\sqrt[]{-1+3}+2=2-\sqrt[]{2}\approx0.5858 \\ g(6)=-\sqrt[]{6+3}+2=-\sqrt[]{9}+2=-1 \end{gathered}`

We plot these points:

We see from this plot that there are two points where f(x) = g(x).